Toolkit: Mass / Energy Balance

Dr. James Doss-Gollin

Thu., Sep. 12

Motivation

  1. Energy systems create lots of \(\text{CO}_2\) emissions
  2. Non-carbon energy sources are now the cheapest way to generate electricity in most places
  3. intermittency is a challenge

Expectations

  1. No exam on this content
  2. Will be useful for your projects
  3. Foundational idea in your other classes as well!

Unifying Theories

Today

  1. Unifying Theories

  2. Mass and Energy Balances

  3. Examples

Conservation of Matter

  1. Without nuclear reaction matter can neither be created nor destroyed
  2. Form and properties of matter can, of course, change
  3. Example: glass of water left out
  4. Mathematical representation is mass balance

Conservation of energy

  1. Energy can neither be created nor destroyed
  2. Energy can be transformed from one form to another
  3. Example: chemical energy in gasoline is converted to kinetic energy in a car
  4. Mathematical representation is energy balance

Conservation of matter and energy

In 1905, Einstein showed that mass and energy are equivalent. This is relevant for nuclear reactions, but generally not something we need to worry about for most civil and environmental systems on Earth.

Mass and Energy Balances

Today

  1. Unifying Theories

  2. Mass and Energy Balances

  3. Examples

Accounting perspective

\[ \text{Accumulation} = \sum\text{Input}_i - \sum\text{Output}_i \] where accumulation, input, and output refer to the mass or energy accumulating in the system or flowing into or out of the system.

Control Volume

  1. We need to define “the system”
  2. Start with conceptual understanding, such as a sketch
  3. Draw boundaries around the system to define what is the control volume
  4. There is an art to clever choices of the control volume to make calculations simpler

Time-Varying Accumulations

Often inputs and outputs are time-varying \[ \text{Rate of Accumulation} = \text{Rate of Input} - \text{Rate of Output} \] where rate means per unit time.

Rates as Derivatives

In calculus we write this as \[ \frac{dM}{dt} = \frac{dM_\text{in}}{dt} - \frac{dM_\text{out}}{dt} \] where \(M\) is the amount of material in the system, \(M_\text{in}\) is the amount of material entering the system, and \(M_\text{out}\) is the amount of material leaving the system.

Accounting for Reactions

  1. When no chemical or biological reaction takes place and no radioactive decay occurs, the substance is conserved.
  2. In many environmental systems, transformations occur within the system
    1. Byproducts such as \(\text{CO}_2\) are formed
    2. Compounds are destroyed (e.)
  3. We account for this by adding a term for the reaction rate. \[ \frac{dM}{dt} = \frac{dM_\text{in}}{dt} - \frac{dM_\text{out}}{dt} + r(\cdot) \]

First-order reaction

In many problems, the rate of reaction is proportional to the amount of material in the system. \[ r(\cdot) = -k M \] where \(k\) is the reaction rate constant.

Making some assumptions (complete mixing, etc) the total mass \(M\) is \(C\) (concentration) times \(V\) (volume). \[ \frac{dM}{dt} = d(CV)/dt = V dC/dt \]

\[ \frac{dM}{dt} = \frac{d M_\text{in}}{dt} - \frac{d M_\text{out}}{dt} - k CV \]

First-order reaction with no input or output

If there are no inputs or outputs, and things are well-mixed, then \[ r = -kC = \frac{dC}{dt} \] ::: {.fragment} If we integrate this out, we can get an expression for the concentration as a function of time. \[ C(t) = C_0 e^{-kt} \] :::

Units of energy

  1. Energy has many forms (thermal, mechanical, kinetic, potential, electrical, chemical, etc…)
  2. SI units are \(\text{J}\) (Joules), but heat units are also used (e.g., calorie)
  3. Specific heat of a substance is the amount of heat required to increase a unit mass by one degree, expressed in units of \(\text{energy} \times \text{mass}^{-1} \times \text{temperature}^{-1}\)

Examples

Today

  1. Unifying Theories

  2. Mass and Energy Balances

  3. Examples

Rainwater harvesting

Ceará, Brazil, 2014

Mass balance for water:

  • In: rainwater
  • Out: consumption (leak? evaporation?)
  • Maximum volume is fixed

Could also perform mass balance for substances in water (bacteria, dust, etc.)

Thermal energy storage

[MIT Technology Review]

Batch reactor

AG Scientific

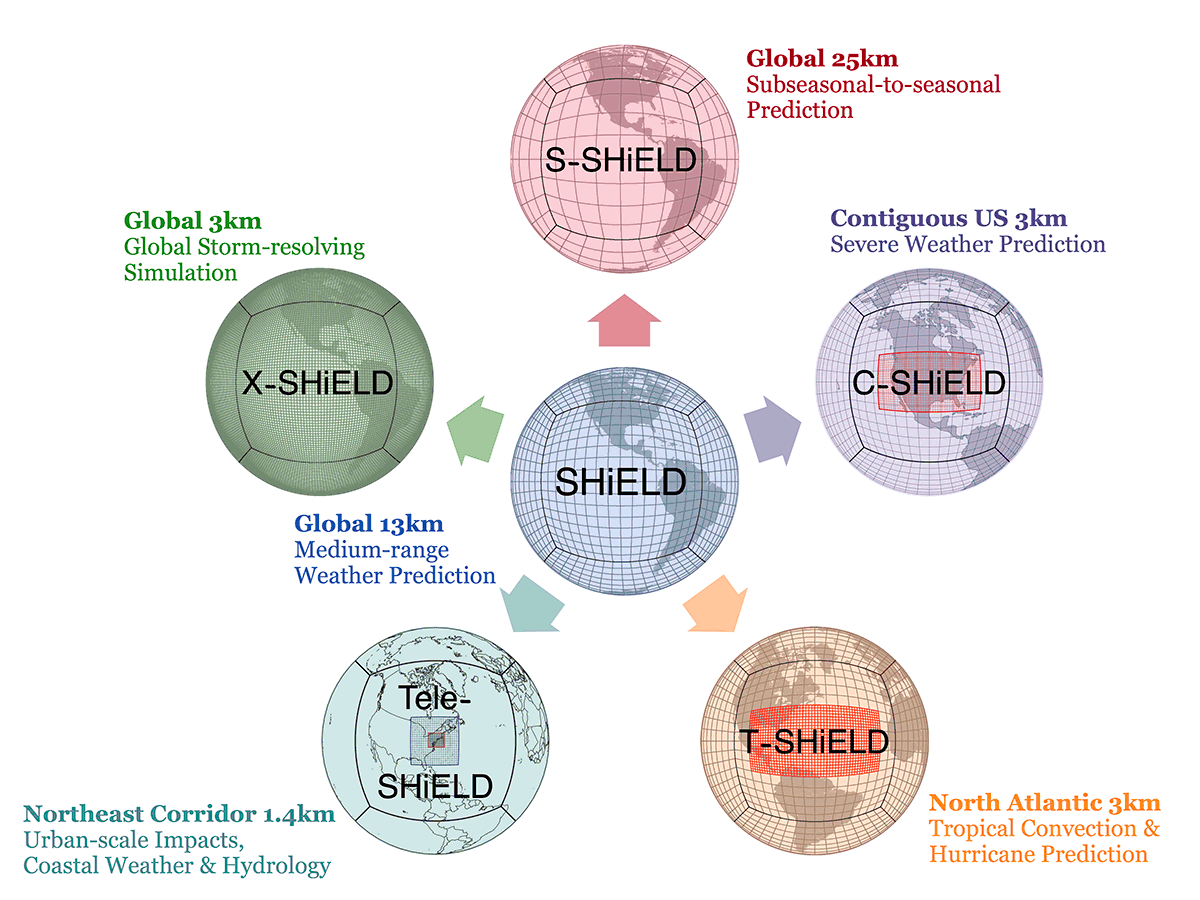
Weather prediction

NOAA GFDL

Nutrient cycles

Washington State Department of Ecology

See Khan Academy videos on Phosphorus and Nitrogen cycloes

Wrapup

  1. Tuesday: short class on energy storage technologies
  2. Thursday:
    1. Group one-pagers due
    2. Instructions on project 1 write-up and presentation given
    3. Reproducibility and transparency with computers