Statistics for Climate Risk Management

James Doss-Gollin

September 14, 2023

Follow along

jdossgollin.github.io/presentations-site

Download as PDF:

  1. Navigate to the presentation
  2. Press e to print

Works best on Chrome / Brave. Detailed instructions here

How do we use probabilities?

Today

  1. How do we use probabilities?

  2. Where do we get probabilities?

How do we manage climate risks?

  1. Reduce emissions to prevent future climate change (“mitigation”)
  2. Real-time monitoring and forecasting
  3. Building codes and design standards
  4. Insurance
  5. …

Sizing a stormwater pipe

  1. Rainfall-runoff model
    • rational method: \(Q= C i A\) where \(i\) is rainfall intensity, \(A\) is area, and \(C\) is runoff coefficient
  2. Common standard: \(\Pr \left\{i > i^* \right\} = 1/T\)
    • Annual probability that \(i > i^*\) is \(1/T\)
  3. Size your culvert to handle \(Q^* = Ci^*A\)
  4. Requires knowing \(p(i)\)!
    • Probability distribution of \(i\)

Drainage installation

Floodplain mapping in a riverine system

  1. Estimate the 99th percentile (100 year return level) of annual maximum streamflows \(Q\)
  2. Use a hydraulic model to model where the water goes
  3. Requires knowing \(p(Q)\)

Floodplain in Selinsgrove, PA

Index insurance pricing

  1. Index insurance: if some index \(I\) is above a threshold \(I^*\), pay out \(X\)
    • Total rainfall in a season, area flooded, etc
  2. Let \(p^* = \Pr \left\{I > I^* \right\}\) is the probability of a payout
  3. Naive pricing uses a point estimate of \(p^*\): \(\frac{R}{X} = \mathbb{E} \left[ p^* \right]\)
  4. Risk pricing accounts for uncertainty in estimating \(p^*\): \(\frac{R}{X} = \mathbb{E}[p^*] + \lambda \mathbb{V}^{1/2}[p^*]\)
    • Requires knowing \(p(p*)\)!

Social cost of carbon

A chain of conditional probabilities:

  1. \(p \left( CO_2 \, \mid \, \text{policy} \right)\)
  2. \(p \left( T \, \mid \, CO_2 \right)\) (climate sensitivty)
  3. \(p \left( \text{local hazard} \, \mid \, T \right)\)
  4. \(p \left( \text{damages} \, \mid \, \text{local hazard} \right)\)

Important point

Choices of which damages to value (and to whom) matters a lot (Errickson et al., 2021)!

Other decisions use probabilities

  1. Seasonal electricity resource adequacy (Doss-Gollin et al., 2021)
  2. Levee design (Garner & Keller, 2018)
  3. Water supply planning (Fletcher et al., 2019)
  4. Multihazard design (Bruneau et al., 2017)
  5. etc…

Caveat

This is not to neglect the importance of epistemic or deep uncertainties whose probability distributions cannot be objectively determined.

Where do we get probabilities?

Today

  1. How do we use probabilities?

  2. Where do we get probabilities?

Example: storm surge

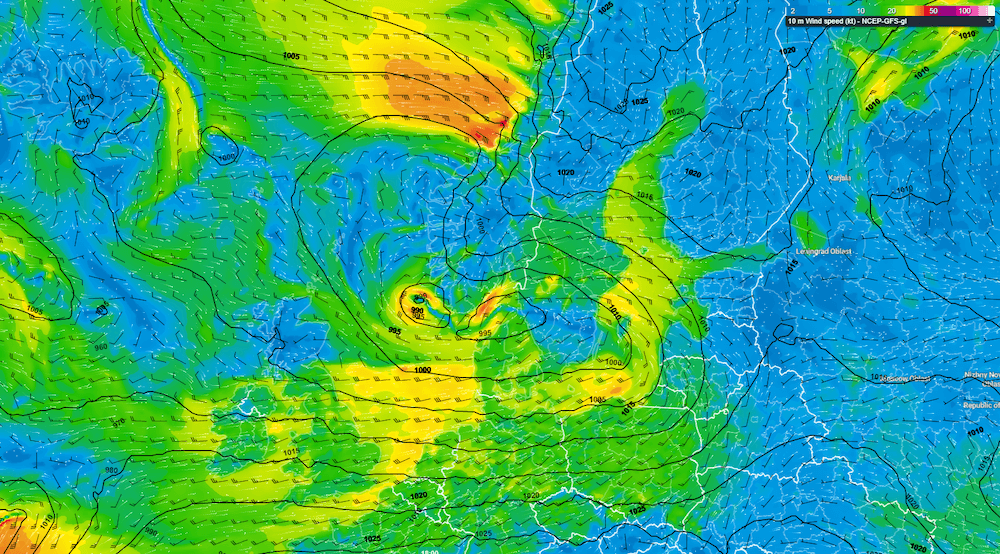
Waves Synoptic Forecast

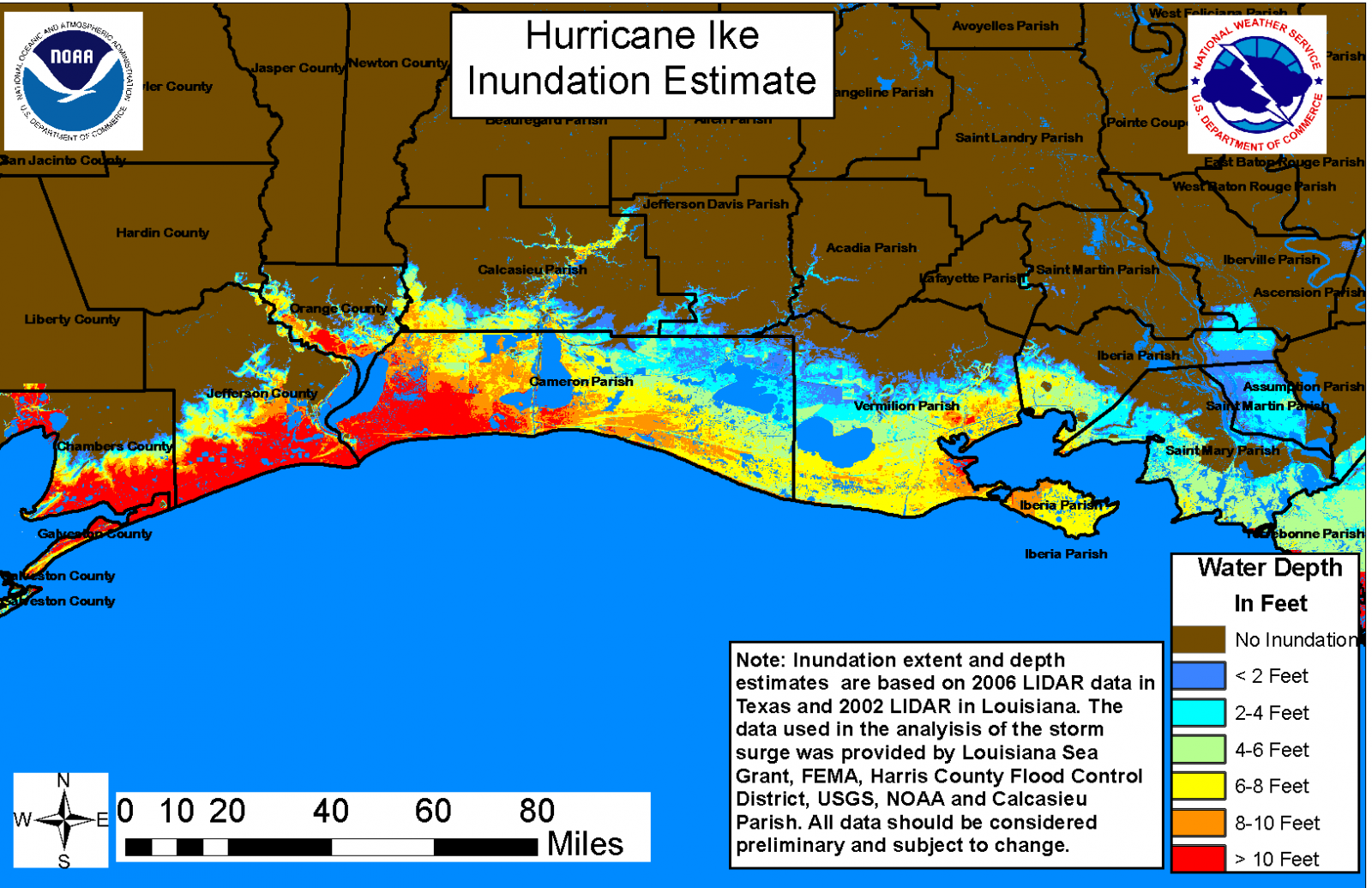
Ike flood depths Ike path

Problem statement:

You are have been comissioned by a small coastal community to quantify the probability distribution of storm surge heights at their location. This knowledge will help them identify properties at risk of flooding, update zoning codes, and plan for future development.

Estimate probability from historical data

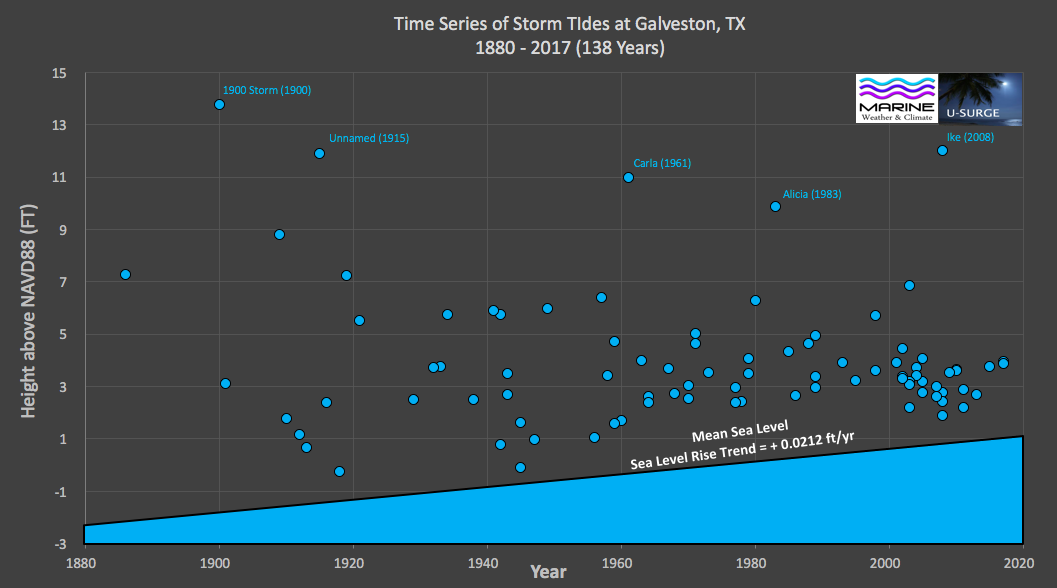
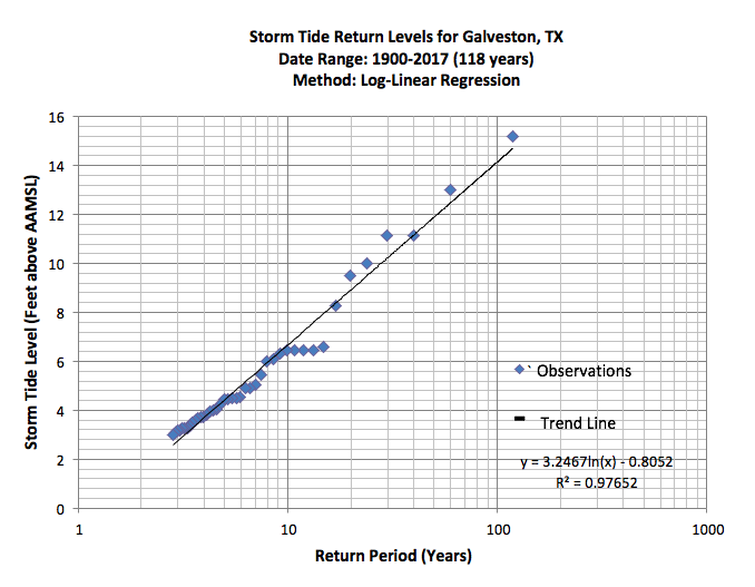
Maximum water levels at Galveston Return levels

Limitations?

  1. No climate change (stationarity)
  2. Short record
  3. ➡️ what is probability of a really big storm?

Tropical cyclone tracks and characteristics

Estimate the probabilty distribution of tropical cyclone characteristics from historical data, conditional on weather data, and generate large numbers of synthetic storms.

Bloemendaal et al. (2020)

Wind and rainfall fields

For our synthetic storms we will need to model the wind and rainfall fields to generate storm surge

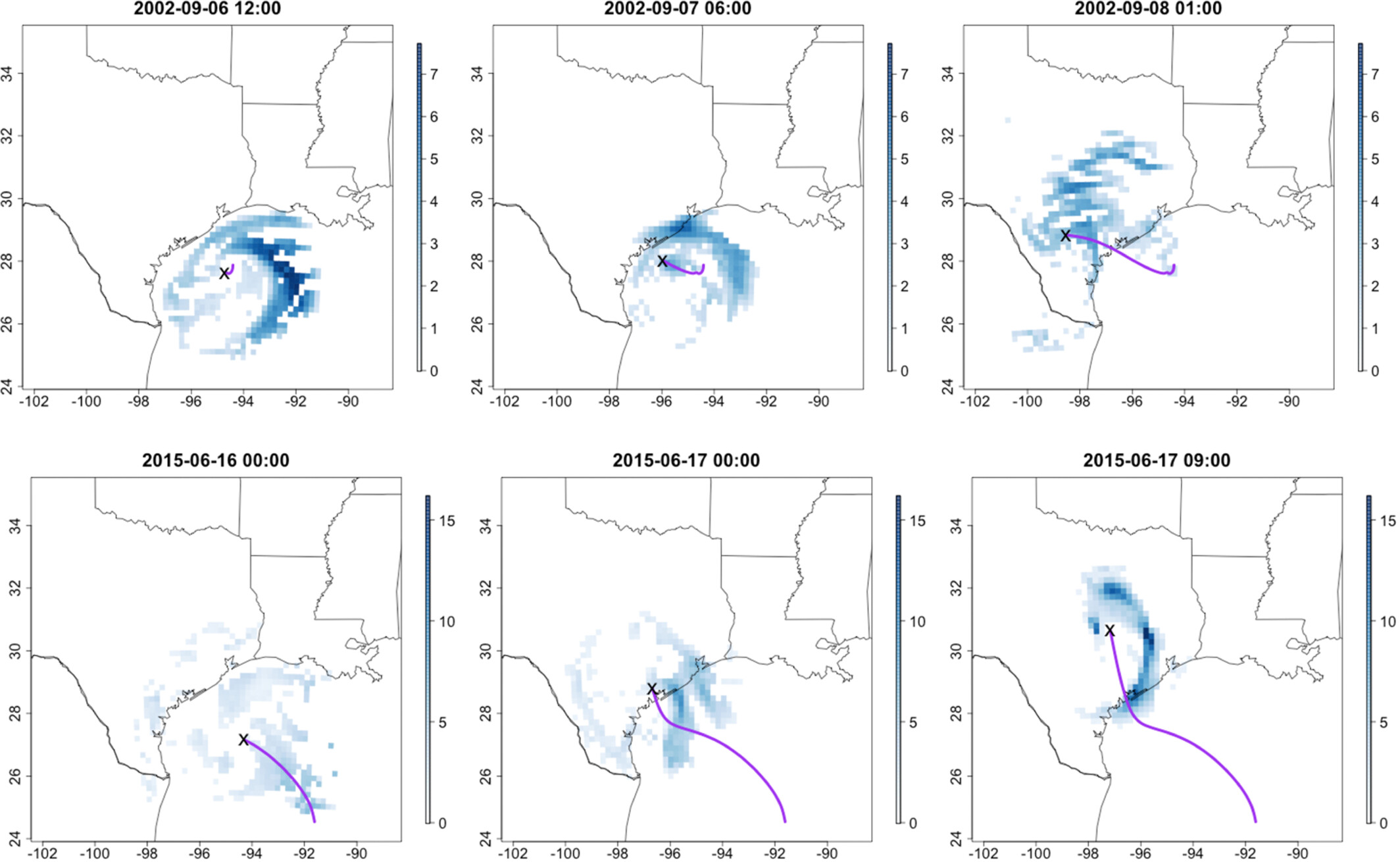
Kleiber et al. (2023)

Sea level

Galveston Relative Sea Level and Projections

What separates the scenarios? To first order:

  1. How much \(CO_2\) we emit
  2. How much the climate system warms in response to \(CO_2\) (climate sensitivity)
  3. Ice sheet response to temperatures

Learn more

  1. Visit dossgollin-lab.github.io
  2. Take CEVE 421
  3. Take CEVE 443 (coming soon)
  4. jdossgollin@rice.edu

References

Bloemendaal, N., Haigh, I. D., de Moel, H., Muis, S., Haarsma, R. J., & Aerts, J. C. J. H. (2020). Generation of a global synthetic tropical cyclone hazard dataset using STORM. Scientific Data, 7(1), 40. https://doi.org/10.1038/s41597-020-0381-2
Bruneau, M., Barbato, M., Padgett, J. E., Zaghi, A. E., Mitrani-Reiser, J., & Li, Y. (2017). State of the art of multihazard design. Journal of Structural Engineering, 143(10), 03117002. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001893
Doss-Gollin, J., Farnham, D. J., Lall, U., & Modi, V. (2021). How unprecedented was the February 2021 Texas cold snap? Environmental Research Letters. https://doi.org/10.1088/1748-9326/ac0278
Errickson, F. C., Keller, K., Collins, W. D., Srikrishnan, V., & Anthoff, D. (2021). Equity is more important for the social cost of methane than climate uncertainty. Nature, 592(7855), 564–570. https://doi.org/10.1038/s41586-021-03386-6
Fletcher, S., Lickley, M., & Strzepek, K. (2019). Learning about climate change uncertainty enables flexible water infrastructure planning. Nature Communications, 10(1), 1782. https://doi.org/10.1038/s41467-019-09677-x
Garner, G. G., & Keller, K. (2018). Using direct policy search to identify robust strategies in adapting to uncertain sea-level rise and storm surge. Environmental Modelling & Software, 107, 96–104. https://doi.org/10.1016/j.envsoft.2018.05.006
Kleiber, W., Sain, S., Madaus, L., & Harr, P. (2023). Stochastic tropical cyclone precipitation field generation. Environmetrics, 34(1), e2766. https://doi.org/10.1002/env.2766