Nonstationary Rainfall Frequency Estimates for Texas

@AGU 2023, NH14B-07

JAMES DOSS-GOLLIN

Rice University
Civil & Environmental Engineering

Yuchen Lu (Rice)

Benjamin Seiyon Lee (GMU)

John Nielsen-Gammon (TAMU)

Rewati Niraula (TWDB)

IDF CURVES UNDERPIN RISK ASSESSMENT

Houston Chronicle

Bates et al. (2021) fig. 8

Mark Wolfe/FEMA News

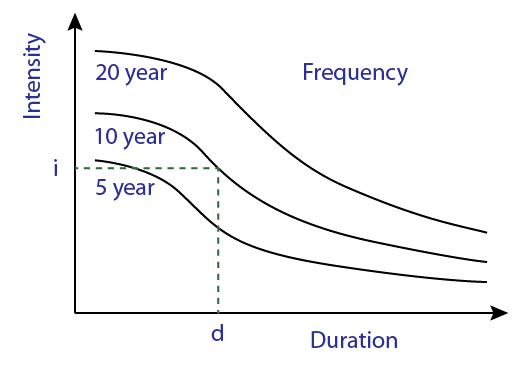
EXISTING GUIDANCE LEAVES GAPS

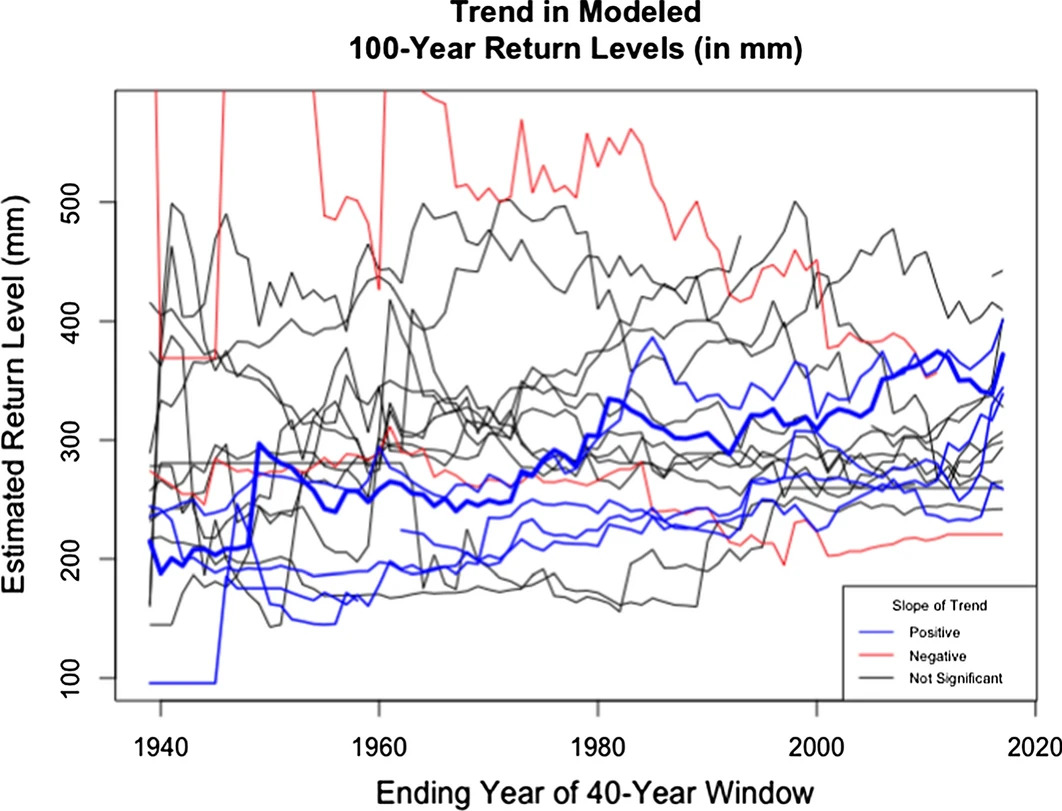
CLIMATE IS CHANGING BUT RANDOMNESS CHALLENGES TREND ESTIMATION

Fagnant et al. (2020): each line is a gauge from the same \(5^\circ \times 3^\circ\) region

NONSTATIONARY MODELS

NEED MORE PARAMETERS

Generic nonstationary model for annual maximum precipitation: \[ y(\vb{s}, t) \sim \text{GEV} \left( \mu(\vb{s}, t), \sigma(\vb{s}, t), \xi(\vb{s}, t) \right) \]

Process-informed models condition parameters on climate indices \(\vb{X}(t)\) (Cheng & AghaKouchak, 2014; Schlef et al., 2023) \[ \theta(\vb{s}, t) = \alpha + \overbrace{\beta(\vb{s})}^\text{more params} \times \overbrace{\vb{X}(t)}^\text{climate} \] for \(\theta \in \{\mu, \sigma, \xi \}\)

NONSTATIONARY MODELS

INCREASE ESTIMATION UNCERTAINTY

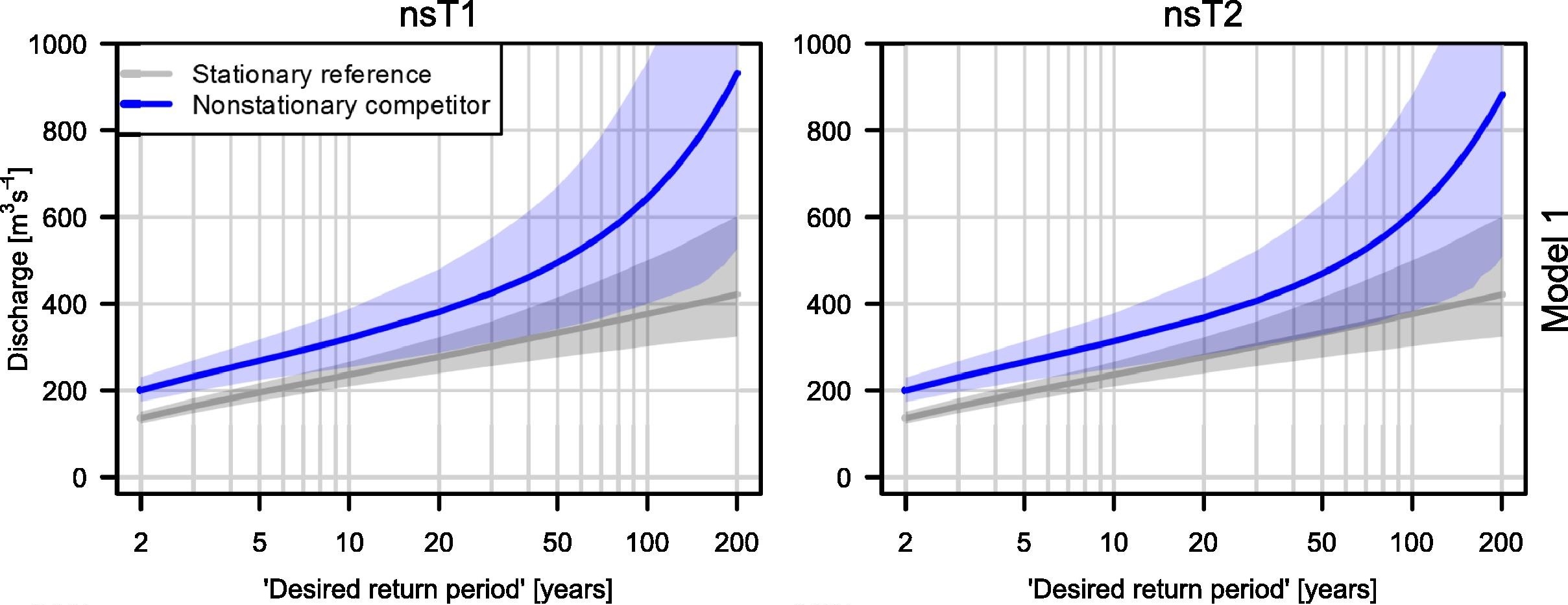
Serinaldi & Kilsby (2015): more parameters, same data āž”ļø posterior uncertainty šŸ“ˆ

MORE/BETTER DATA šŸ¤

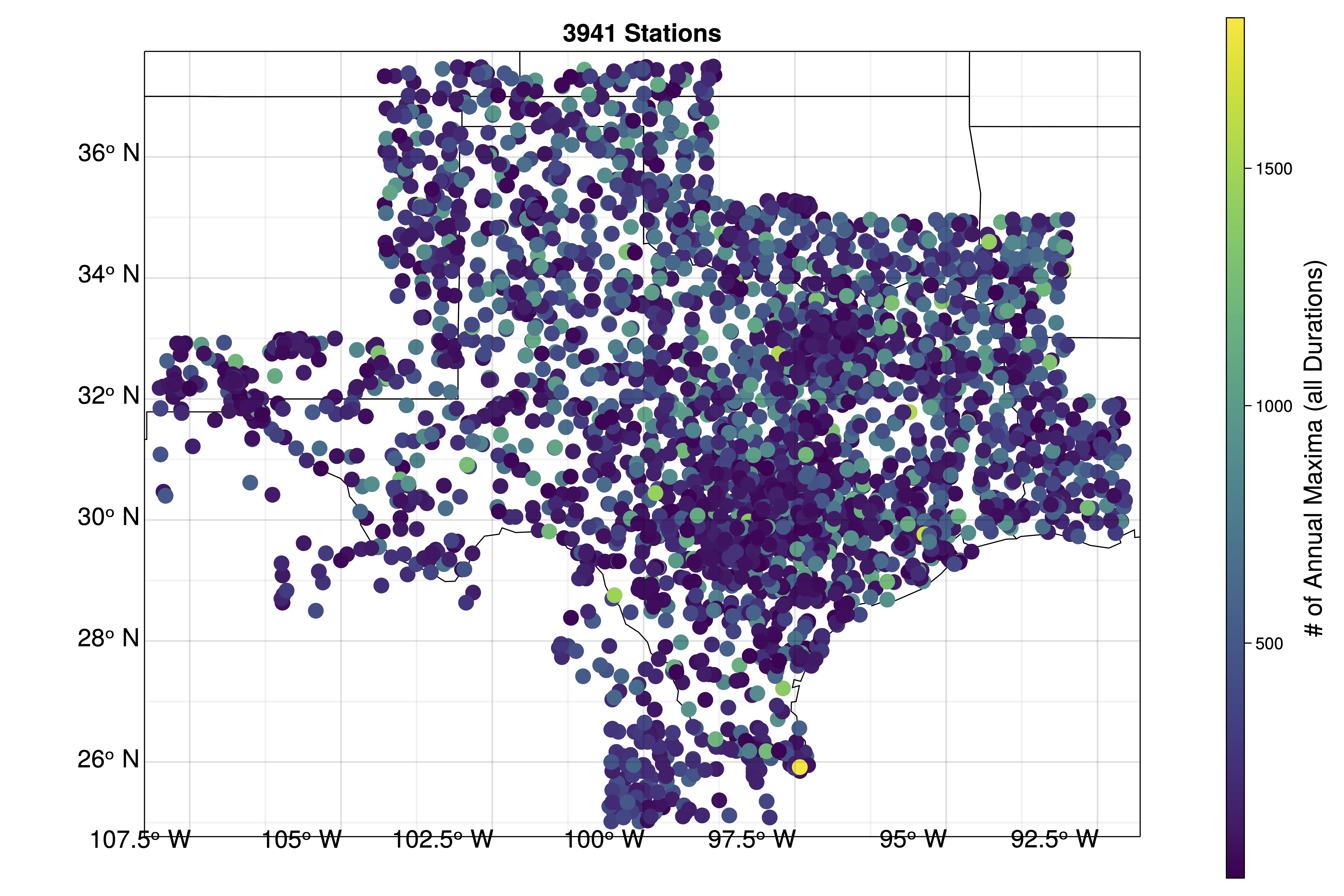
We use long-record gauges AND newer mesonets

SPATIALLY VARYING COVARIATES

  • framework: Bayesian hierarchical model (flexible, probabilistic)
  • hypothesis: parameters are smooth
  • model: latent parameters as spatial fields (Moran basis functions)

CLIMATE CHANGE DRIVES LARGER AND MORE VARIABLE EXTREMES

Show only the increasing trends here:

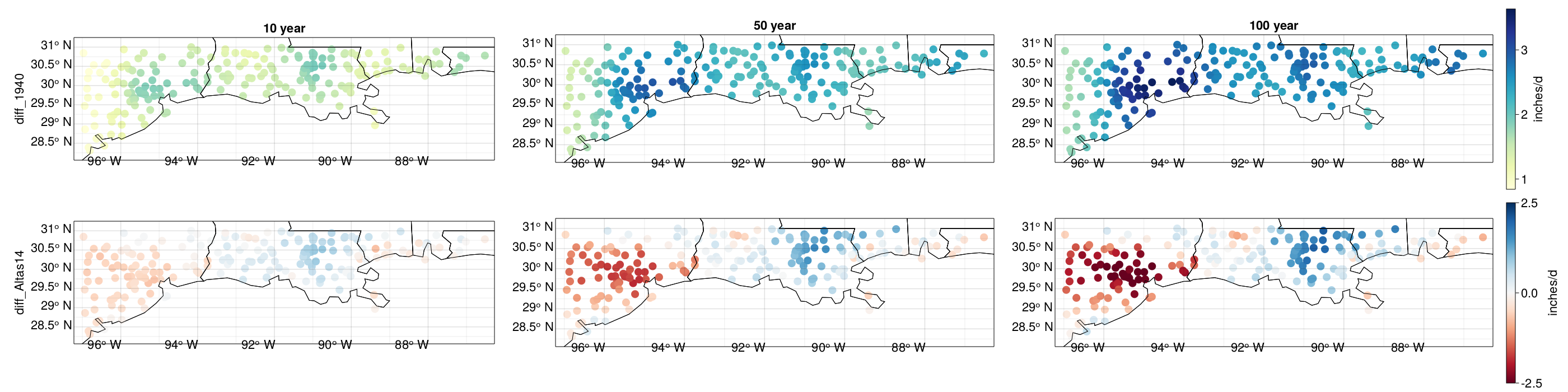
WE FIND HIGHER HAZARD THAN ATLAS-14 EXCEPT IN HARVEY-IMPACTED AREAS

DIAGNOSTICS SUGGEST EXTREME PROBABILITIES ARE WELL-CALIBRATED

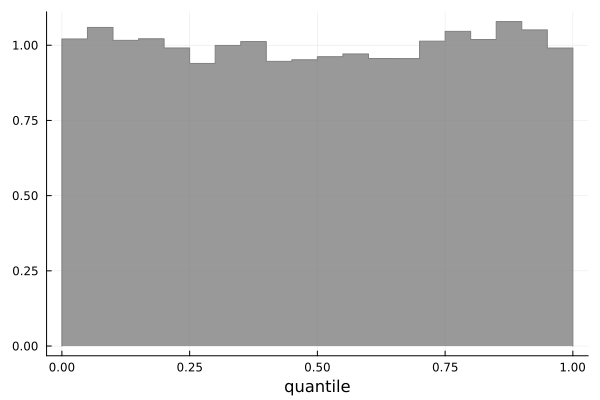
SUMMARY

Bayesian space-time model:

āœ… Reduce estimation uncertainty

āœ… Explicitly spatial (free interpolation)

āœ… Well-calibrated

āŒ Zap sampling variability

References

Bates, P. D., Quinn, N., Sampson, C., Smith, A., Wing, O., Sosa, J., et al. (2021). Combined modeling of US fluvial, pluvial, and coastal flood hazard under current and future climates. Water Resources Research, 57(2), e2020WR028673. https://doi.org/10.1029/2020WR028673
Cheng, L., & AghaKouchak, A. (2014). Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Scientific Reports, 4(1), 7093. https://doi.org/10.1038/srep07093
Fagnant, C., Gori, A., Sebastian, A., Bedient, P. B., & Ensor, K. B. (2020). Characterizing spatiotemporal trends in extreme precipitation in Southeast Texas. Natural Hazards, 104(2), 1597ā€“1621. https://doi.org/10.1007/s11069-020-04235-x
Schlef, K. E., Kunkel, K. E., Brown, C., Demissie, Y., Lettenmaier, D. P., Wagner, A., et al. (2023). Incorporating non-stationarity from climate change into rainfall frequency and intensity-duration-frequency (IDF) curves. Journal of Hydrology, 616, 128757. https://doi.org/10.1016/j.jhydrol.2022.128757
Serinaldi, F., & Kilsby, C. G. (2015). Stationarity is undead: Uncertainty dominates the distribution of extremes. Advances in Water Resources, 77, 17ā€“36. https://doi.org/10.1016/j.advwatres.2014.12.013

Limitations of Climate Models